Dr. Dmitri Kopeliovich

Hydrodynamic journal bearing is a bearing operating with hydrodynamic lubrication, in which the bearing surface is separated from the journal surface by the lubricant film generated by the journal rotation.

Most of engine bearings are hydrodynamic journal bearings.

• Journal bearing operation
• Reynolds Equation
• Engineering calculations of journal bearing performance

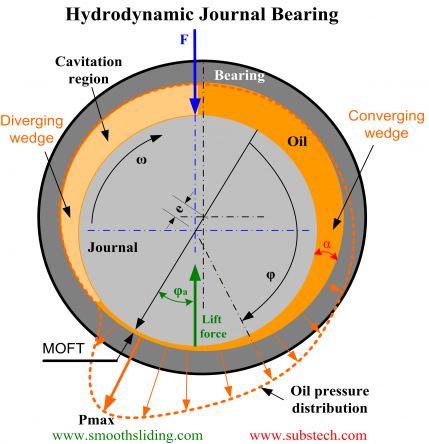
The figure demonstrates a hydrodynamic journal bearing and a journal rotating in a clockwise direction.
Journal rotation causes pumping of the lubricant (oil) flowing around the bearing in the rotation direction.
If there is no force applied to the journal its position will remain concentric to the bearing position. However a loaded journal displaces from the concentric position and forms a converging gap between the bearing and journal surfaces.
The pumping action of the journal forces the oil to squeeze through the wedge shaped gap generating a pressure.
The pressure falls to the cavitation pressure (close to the atmospheric pressure) in the diverging gap zone where cavitation forms.

According to Michael M. Khonsari and E. Richard Booser two types of cavitation may form in journal bearing:

• Gaseous cavitation associated with air and other gases dissolved in oil. If the oil pressure falls below the atmospheric pressure the gases tend to come out of the oil forming gaseous cavitation voids. The cavities are carried by the circulating oil to the pressurized converging gap where they redissolve in the oil and disappear without any damaging effect.
• Vapor cavitation forms when the load applied to the bearing fluctuates at high frequency (e.g. bearings in high RPM internal combustion engines). The oil pressure instantly falls causing formation of cavities due to fast evaporation (boiling). When the pressure rises the vapor cavities (cavitation bubbles) contract at high velocity. Such collapse results in impact pressure, which may erode the bearing material.

The oil pressure creates a supporting force separating the journal from the bearing surface.
The force of oil pressure and the hydrodynamic friction force counterbalance the external load F.
The final position of the journal is determined by the equilibrium between the three forces.
In the hydrodynamic regime the journal “climbs” in the rotation direction (left side of the bearing).
If the journal works in boundary and mixed lubrication the hydrodynamic pressure force disappears (the other two forces remain). Thus, the “climbing” direction is opposite to the rotation direction and the journal rolls up the right side of the bearing.

to top

Lubricant pressure distribution as a function of journal speed, bearing geometry, oil clearance and lubricant viscosity is described by Reynolds equation:


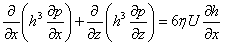
Where:
h – local oil film thickness,
η – dynamic viscosity of oil,
p – local oil film pressure,
U – linear velocity of journal,
x - circumferential direction.
z - longitudinal direction.

Close form solution of Reynolds equation can not be obtained therefore finite elements method is used to solve it.

Analytical solutions of Reynolds equation exist only for certain assumptions:

• Sommerfeld Solution
  

The equation is solved with the assumption that there is no lubricant flow in the axial direction (infinitely long bearing assumption).

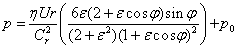
• Ocvirk Solution
  

Ocvirk solution for infinitely short bearing assumption neglects circumferential pressure gradients (first term of Reynolds equation).

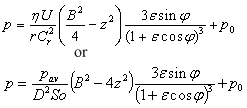
Where:

C_r – radial clearance C_r = (D-D_j)/2,
r – bearing radius,
D_j - journal diameter,
ε - eccentricity ratio ε = e/C_r
e - absolute bearing eccentricity,
B – bearing length,
p₀ - cavitation pressure,
So - Sommerfeld number (see below).

Sommerfeld and Ocvirk solutions are applicable only in the region of positive pressure.

to top

Engineering analysis of a journal bearing performance may be made by using Raimondi-Boyd charts containing numerical solutions of Reynolds equation for bearings with different length-to-diameter ratio.

These engineering calculations are based on the dimensionless bearing parameter called Sommerfeld number:

So = F Ψ²/(DBωη)

Where:

F – bearing load,
Ψ – relative bearing clearance Ψ = (D-D_j)/D,
B – bearing length,
D – bearing diameter,
D_j - journal diameter,
η – dynamic viscosity of oil,
ω – angular speed of journal.

Raimondi-Boyd analysis is based on the assumption that the oil viscosity does not change when it passes through the bearing. Since the real oil heats up in the bearing and its viscosity drops it is assumed that oil viscosity is determined at the effective temperature T_eff = T_en + 0.5ΔT_as (ΔT_as is assumed temperature rise).

The calculation procedure is as follows:

1. Temperature rise ΔT_as is assumed.
2. Effective temperature T_eff = T_en + 0.5ΔT_as
3. Oil viscosity η at the temperature T_eff is determined (viscosity-temperature chart).
4. Relative bearing clearance is calculated Ψ = (D-D_j)/D
5. Sommerfeld number is calculated: So = F Ψ²/(DBωη)
6. Values of Sommerfeld number and geometry parameter B/D determine the bearing eccentricity ε, which is obtained from the eccentricity chart ε(So, B/D).
7. Minimum oil film thickness h_min = 0.5DΨ(1 – ε)
8. Eccentricity value and the geometry ratio B/D are used for determination specific coefficient of friction f’(ε, B/D), angular position of the minimum oil film thickness φ(ε, B/D) and oil flow parameter Q’(ε, B/D).
9. Coefficient of friction f = f’Ψ
10. Oil flow rate Q = D³ωΨQ’
11. Power loss due to friction P = fFωD/2
12. Calculated oil temperature rise ΔT_ca = P/(cQ) where c is specific heat capacity of oil
13. Calculated oil temperature rise ΔT_ca is compared to the assumed value ΔT_as and if there is a significant difference between them a new assumption of the temperature rise is made.

The above calculation procedure is repeated for several iterations until the calculated and assumed values of the temperature rise become equal.

to top

• Bearings in internal combustion engines
• Engine parameters determining bearing loading
• Lubrication regimes
• Hydrodynamic lubrication theory
• Geometrical parameters of engine bearings
• Mechanisms of wear
• Requirements to engine bearing materials
• Engine bearing fatigue test
• Engine bearing materials
• Copper based bearing materials
• Manufacturing bi-metal strips for copper bearings
• Aluminum based bearing materials
• Continuous casting of aluminum based bearing alloys
• Manufacturing bi-metal strips for aluminum bearings
• Lead based engine bearing overlays
• Tin based engine bearing overlays
• Sputter bearing overlays
• Polymer based engine bearing overlays
• Engine bearing failure
• Selection of engine bearing materials
• Effect of low viscosity oils on engine bearings
• pMax Black™ - Strengthened Tri-metal Bearing Materials for High Performance Bearings
• U-Groove™ Modified Design of Oil Groove for High Performance Bearings
• ElliptiX™ Oil Hole of New Design for High Performance Bearings
• EccentriX™ Optimal Eccentricity for High Performance Bearings
• RadiaLock™ - Design of Crush Height for Reliable Press Fit of High Performance Bearings
• Modern Trends In Materials For High Performance Engine Bearings
• Optimization of Clearance Design for High Performance Engine Bearings
• Camshaft Bearings
• Ecological Aspects Of Engine Bearings
• Consistency in Bearing Wall Thickness
• Soft Strength of Racing Bearings
• Effect of oil viscosity on hydrodynamic friction of engine bearings
• Bearing Materials For Race Engines
• Oil Clearance and Engine Bearings
• Polymer Coated Bearings
• Development of Performance Bearings for Race Engines of Modern Design
• Failures of Engine Bearings and their Prevention
• Engine Bearing Housing and How it Affects Engine Bearings
• Polymer Coatings for Race Engine Bearings
• Heavy Duty Engine Bearings - Materials, Geometry, Failures
• Hydrodynamic Bearing – Calculations and Design
• Geometry of Engine Bearings
• Crush Height of Engine Bearings
• Materials for Engine Bearings
• Engine oils

to Metals
to Engine bearings